Objection’s LSAT Tips – Simple Ordering Games
Question Type: Simple Ordering Games
Section: Logic Games
Introduction
The analytical reasoning, or logic games, section of the LSAT is one of the toughest sections on the test, but also the most learnable. What makes logic games particularly difficult is their highly timed nature – there is no time to waste with four games in 35 minutes. One of the keys to performing well on logic games is being able to quickly identify the question type and the best way to tackle it. Some games will be easier than others, and if you can quickly identify which games in the section are easy to solve, you can do them with confidence and move on to the harder – and longer – games.
The easiest type of game for most is the simple ordering game. In this type of game, you are asked to order a certain number of variables for a corresponding number of slots (e.g. eight variables would fill eight slots) according to the rules given.
Method
There are many different ways to diagram rules; I will not rehash them here. I highly recommend PowerScore’s Logic Games Bible to learn every possible technique.
There are two big keys to ordering games and, actually, all games in general: clear diagrams and inferences.
1. Clear Diagrams – If Carol, Jenny, and Samantha went to the bathroom, and Carol went to the bathroom before Jenny but after Samantha, it is much easier to scribble S – C – J at the bottom of the page than trying to keep track of the rule entirely in your head. You should also strive for neatness. If your diagrams are so messy that you cannot read them, you will either make foolish errors or need to recheck the original rules, wasting time. Clear and neat diagrams, particularly in ordering games, will allow you to answer questions much quicker than you would have been able to otherwise. Time is everything on the LSAT.
2. Inferences – What you can infer from a rule or a combination of rules is often as important as the rules themselves. The rules aren’t random; they all serve some purpose. When one variable is used in more than one rule, it can lead to strong, perhaps “game-breaking” inferences. Though the example above is simple, in a larger game such a rule not only means what it explicitly says, but it can be inferred that neither Carol nor Jenny used the bathroom first.
Games are more easily taught by example, so let’s do one.
Example
A bus drives exactly eight children – F, J, K, L, M, N, O, and P – to school. Each child gets out of the bus, one child at a time. The order in which the children get off the bus is consistent with the following conditions:
M gets out at some time before both O and F.
F gets out at some time after P.
L gets out some time before M but at some time after J.
K gets out at some time after M.
J gets out at some time before N.
After a quick read through of the game and the rules, you should immediately begin inferring and diagramming.
Rule 1 inferences:
F cannot get off first (M must be before it).
M cannot get off last (O and F must be after it).
M cannot get off seventh (both O and F must be after it).
Rule 2 inferences:
F cannot get off first (P must be before it).
P cannot get off last (F must be after it).
Rule 3 inferences:
L cannot get off first (it must be after J).
L cannot get off last (it must be before M).
J cannot get off last (it must be before L).
M cannot get off first (it must be after L).
Rule 4 inferences:
K cannot get off first (it must get off after M).
M cannot get off last (K must be after it).
Rule 5 inferences:
J cannot get off last (it must be before N).
N cannot get off first (J must be before it).
From five rules, it is possible to immediately draw fourteen inferences (although some are redundant). There will be times when you miss an inference. But with time and practice, you will be able to get enough of them to get through most of the problems with ease, allowing you to spend more time working on one that may stumping you due to a missed inference.
I personally use two diagrams for this problem. Both are quick and easy. The first simply orders the variables visually while the other allows me to represent which variables can and cannot be in which slots. Many will find that the first diagram encapsulates everything you will need to answer the questions. Inferences need not be drawn out verbatim if you can figure out everything you need from the first diagram. Here is what the two diagrams I use would look like:
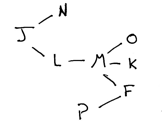
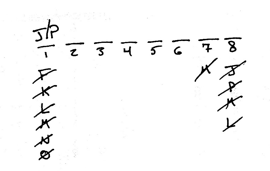
Notice that by eliminating the possibility of many variables from being in the first slot, I was able to narrow down the possibilities to either J or P.
Now with our diagrams in hand, let’s move to the questions:
1. Which one of the following could be the order, from first to last, in which the children get off of the bus?
A) L, P, M, J, N, O, K, F
B) P, J, N, F, L, M, O, K
C) J, N, L, M, F, P, K, O
D) P, N, J, L, M, O, F, K
E) J, N, L, M, P, K, O, F
A – Incorrect. L being first violates rule three. This is quickly seen on our second diagram.
B – Incorrect. F cannot come before L (this violates a combo of rules one and three). This is quickly seen on our first diagram.
C – Incorrect. F cannot come before P. This violates rule two and is easily seen on our first diagram.
D – Incorrect. N cannot come before J. This violates rule five and is easily seen on our first diagram.
E – Correct. No rules violations.
2. Which one of the following could be true?
A) O is the second child out of the bus.
B) J is the third child out of the bus.
C) F is the fourth child out of the bus.
D) K is the fifth child out of the bus.
E) M is the sixth child out of the bus.
(Side note: Questions like this are blessings when they come early, as they allow you to add any inferences you may have missed to your diagram.)
A – Incorrect. As seen in our first diagram, there must be at least three children before O, making fourth the earliest possible exit for O.
B – Incorrect. As seen in our first diagram, there are six children who must come after J (N, L, M, O, K, F). Placing J third won’t leave enough room since there are only eight slots. The latest J could exit is third. C – Incorrect. F has J, L, M, and P coming before it, as seen in our first diagram. F cannot exit until at least five.
D – Correct. No rules or diagrams violated.
E – Incorrect. Three children must exit after M. The latest M can exit is fifth.
3. If P is the 7th child to get off the bus, then which one of the following could be true?
A) J is the second child off the bus.
B) L is the fourth child off the bus.
C) N is the fifth child off the bus.
D) M is the sixth child off the bus.
E) O is the eighth child off the bus.
A mini-diagram next to the problem is often helpful for hypotheticals like this:
J_ __ __ __ __ __ P_ F_
Plugging P into slot 7 means F is in slot 8 (as F must come after P). This eliminates answer choice E. Also, J must be in slot 1 as P and J are the only two that can exit first.
This eliminates answer choice A.
A – Incorrect. If P is seventh, J must be first (see our second diagram). Those are the only two that can exit first.
B – Incorrect. If L exits fourth, there is not enough room for M, O, and K to exit after L, since time slots 7 and 8 are occupied by P and F.
C – Correct. This is a possibility (i.e. it could be true).
D – Incorrect. This leaves no room for O and K since 7 and 8 are occupied by P and F.
E – Incorrect. F must be in slot 8.
4. If L is the fourth child to get off the bus, which one of the following must be true?
A) J is the first child off the bus.
B) P is the second child off the bus.
C) N is the third child off the bus.
D) M is the fifth child off the bus.
E) O is the seventh child off the bus.
It is in questions like this where the diagrams really serve their purpose. Process of elimination would be difficult because every answer choice could be true, forcing you to plug variables into different slots trying to prove each one false. It’s easier to just find out which answer choice must be true. If I were actually taking the test, I would not go through each answer choice individually; I would simply find the one which must be true. For the purposes of this tutorial, however, I will go through each possibility.
A – Incorrect. The first three slots could be filled by P, J, and N, in that order, without any rules violations.
B – Incorrect. As we see directly above, P could be first off the bus.
C – Incorrect. Another possibility for the first three slots could be J, N, and P. So N need not be in the third slot.
D – Correct. Since L is in the fourth slot, P, J, and N must come before L. That leaves M, K, O, and F for the last four slots. By looking at our first diagram, we can determine that M must come before all of these. Therefore, M must be in the fifth slot.
E – Incorrect. O could be in the seventh slot, but so could K or F.
5. If F is the fifth child to get off the bus, then each of the following could be true EXCEPT:
A) P is the first child to get off the bus.
B) L is the second child to get off the bus.
C) M is the third child to get off the bus.
D) N is the fourth child to get off the bus.
E) O is the sixth child to get off the bus.
The key phrase in this problem is “could be true EXCEPT”. This means that four of the answer choices could be true and one of them must be false. It is easier to identify the “must” than it is to eliminate the “could’s”.
F being the fifth child off the bus will force one of these answers to be incompatible with our diagrams. But which one? Looking at the diagrams, you can see that at least four children must get off the bus before F: J, L, M, and P. If F gets off fifth and four children must get off before it, then those four must occupy the four slots prior to F. That leaves N, K, and O for slots 6-8 (not necessarily in that order). Now scan the answers and see if there is any answer that puts something other than J, L, M, or P in slots 1-4 or N, K, or O in slots 6-8. In answer choice D, N is placed in slot four. Therefore, D must be false and is the correct response.
6. If J is the second child off the bus, which of the following must be true?
A) K gets off the bus before L.
B) L gets off the bus before N.
C) N gets off the bus before M.
D) O gets off the bus before F.
E) P gets off the bus before N.
While our diagrams make this easy, process of elimination would make this unnecessarily hard. In the second diagram, we can see that only J or P can get off the bus first. If J is the second child, this means that P must be the first child of the bus. Therefore, P gets off the bus before every other child, including N, which is stated in answer choice E.
7. If M gets off the bus some time before P does, then which one of the following could be true?
A) J is the second child off the bus.
B) L is the fourth child off the bus.
C) F is the fourth child off the bus.
D) M is the fifth child off the bus.
E) P is the sixth child off the bus.
These types of questions are difficult since you can’t simply look for a “must” on the diagram because the question asks what could be true. This means, however, that four of the answer choices must be false and a good diagram makes the elimination of several answers relatively simple.
A – Incorrect. If M is before P, P cannot come first. Since J and P are the only children that can be first, J must be first.
B – Incorrect. If L is fourth, M must be fifth, and O, K, and F must occupy slots 6, 7, and 8 (since M must come after T but before O, K, F). Since M is in slot 5 and 6, 7, and 8 are occupied, M cannot come before P.
C – Incorrect. F cannot come fourth and a quick look at the first diagram shows this. J, L, M, and P must come before F. If F is fourth, there is not enough room for those four children.
D – Incorrect. If M gets off the bus before P, and M is fifth, that means P occupies either slot 6 or 7 (it cannot occupy 8, as per the second diagram). This leaves only two slots after M, but M must come before O, K, and F. There would not be enough room for those three.
E – Correct. P being sixth violates no rules.
Final NotesThis is only one example and it is relatively simple and straightforward. Many simple ordering games will seem to be much more complex, but the diagramming process and the thought structure that you applied to the above example are applicable to every simple ordering game. Do not get bogged down by wordiness or lots of variables. Stay calm and clearheaded and methodically work through the problem. Master the basics and the complex will fall in time.
Again, I recommend purchasing a book with LSAT Logic Game diagramming techniques. The most popular is the Logic Games bible.
Also, if you have any questions, please visit the TLS LSAT Prep forum at http://www.top-law-schools.com/forums/viewforum.php?f=6 .
Ken's Introduction to the LSAT
Conquering the LSAT
How I Scored a 180 - Article #1
How I Scored a 180 - Article #2
How I Scored a 180 - Article #3
Retaking the LSAT
Logic Fundamentals: A Lesson In Conditional Reasoning
Objection’s LSAT Tips – “Describe” Questions (LR)
Objection’s LSAT Tips – “Main Point” Questions (LR)
Objection's LSAT Tips - "Must Be True" Questions (LR)
Objection’s LSAT Tips – “Role” Questions (LR)
Objection’s LSAT Tips – “Level Ordering” Games
Objection’s LSAT Tips – “In/Out” Games
Objection’s LSAT Tips – “More/Less” Ordering Games
Objection’s LSAT Tips – Simple Ordering Games
Objection’s LSAT Tips – Multiple Group Games
LSAT Prep with Work and School
LSAT Test Dates for 2019-2020
LSAT Test Dates for 2022-2023
