Law School Investment for Dummies (Now w/ Link) Forum

[Bronte]

It’s a stressful year to be applying to law school. Although the pessimism seems to have passed its peak, there’s still a lot of uncertainty associated with the law school investment. Although we spend plenty of time analyzing the merits of law schools based on a myriad of factors, some more subjective than others, I figured I’d do my part to add a bit of economic rigor to the discussion.

This article outlines two approaches to analyzing the law school investment. Both approaches will employ an Excel spreadsheet, the set-up of which I will walk through step-by-step. For many of you, this will be too boring and tl;dr. For others, I hope it will be a worthwhile tool.

LINK TO DOWNLOAD: Version 1.1 (LinkRemoved) (click "More" > "Download", courtesy of pizzaface)

DISCLAIMER: For educational purposes only. Does not constitute financial advice. Work in progress; may contain material errors. Do not make life decisions based on these rough spreadsheets. All inputs are dummy variables. Models require customization to be meaningful.

LIST OF WORKING ISSUES AND ERRORS

Approach 2

(1) CORRECTED. The first version had a material error in cell B29. The current version is corrected. See below.

(2) TEMPORARY FIX. The old version did not take into account increase in salary after law school. Version 1.1 sets the after law school salary to grow at the same rate you set your initial salary to grow at (cell B7, default = 4%). See the description of this fix on the second page of this thread. A more sophisticated solution may be employed later.

(3) WORKING. The current approach does not take into account the economic value of LRAPs (which, in their basic form, can be seen as a cash-or-nothing put option). I'm working on a method, although it may never come due to estimation difficulties. One should nevertheless take this into account.


Approach 1: The Pragmatic Approach

This approach will simply calculate the average salary necessary to service one’s loan. Specifically, given the desired term of the loan, the desired net income, the interest rate, and, of course, the loan amount, we will calculate the required average annual salary over the term of the loan. Here’s a screenshot of the spreadsheet:



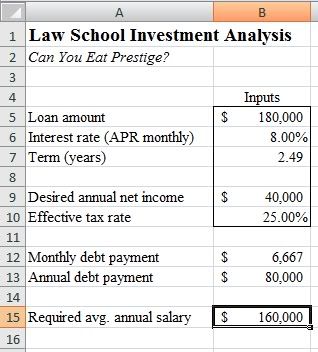
Inputs:

In cell B5, B6, and B7, enter the loan amount, the interest rate expressed in decimal form, and the term, respectively. The loan amount is the total dollar value you will borrow to finance law school. The interest rate is the annual percentage rate (APR) with monthly payments--a standard consumer rate quote. The term is the length of time over which you hope to pay back the loan. For now, enter an 8.00% interest rate and a 10 year term.

In cell B9 enter your desired annual net income. This is the average after-tax, after-loan payment income that you think you’ll need in order to cover living expenses during the term of the loan. In cell B10, enter the effective tax rate. Twenty-eight percent is probably a conservative estimate.

Outputs:

In cell B12, enter the equation: =-PMT(B6/12,B7*12,B5,0). In cell B13, enter the equation: =B12*12. In cell B15, enter the equation: =(B9+B13)/(1-B10).In cell B15, you now have the average annual salary that you will have to earn over the term of the loan to meet your debt payments and have the net income you specified. Fiddle with the inputs.


Approach 2: The Economic Value Approach

This approach is adapted from Vanderbilt Law Professor Herwig Schlunk’s paper “Mamas Don’t Let Your Babies Grow Up To Be…Lawyers” (http://ssrn.com/abstract=1497044). However, it is in no way endorsed by Prof. Schlunk and may materially deviate from his approach as outlined in the paper. It is a much more rigorous approach consistent with theoretical economic analysis. As such, it may seem overly abstract to some people. In particular, its heavy reliance on opportunity costs can be confounding. However, it is quite rational and more sophisticated than the former approach.



In cells B6 and B7, enter the tax rate and projected annual earnings growth, respectively. Again, we’ll use a 28% tax rate. For earnings growth, we’ll use a conservative 4% consistent with a number just above historical inflation rates. In cell C10, enter the annual salary you would have gotten if you did not go to law school. For some, this will be a projection. For others, who are quitting a job to go to law school, this will be more concrete.

In cell D10, enter the exact equation: =C10*(1+$B$7). Select cell D10. Then click on the bottom right corner and drag right until you reach column F. In cell C11, enter the equation: =C10*$B$6. Drag right to column F. In cell C12, enter the equation: =C10-C11. Drag right to column F. In cell C15 and C16, enter the annual tuition expense and estimated cost of books and supplies. Do not include living expenses. Drag both cells right to column E.

In cell C17, enter the equation: =SUM(C15:C16). Drag right to column E. In cell C20, D20, and E20, enter project annual summer earnings. To be conservative given economic conditions, these might be set to zero. In cell C22, enter the equation: =C12+C17-C20. Drag right to column E.

In B25, enter the discount rate. Start with 10%. This is arguably the most controversial input. Schlunk came under some criticism for using excessive estimates. In finance and economics, a discount rate is the rate that could be earned on investment of similar riskiness. Suffice it to say that there is no easy estimate for this figure in this scenario. In B26, enter your estimated career length as an attorney. I used 35 years (yikes). In cell B28, enter an estimated starting salary as a lawyer. This is a dummy variable for now, just use $70,000.

EDIT: To correct error. Cell B29 now has a new equation (see bold). Also, add a "second bracket" effective tax rate in cell C6. This is an estimate of your after-law school tax rate. (Some might note a circular problem here, but we'll ignore it.) Cell B31 has been changed in Version 1.1. See the second bolded equation below.

In cell B29, enter the equation: =B28*(1-C6)-F12. In cell B31, enter the equation: =(B29/(B25-B7))*(1-((1+B7)/(1+B25))^B26)*(1+B25)). In cell C33, enter the equation: =-C22. Drag right to column E. In cell F22, enter the equation: =B31. In cell B34, enter the equation: =NPV(B25,C33:F33).

Finally, we solve for the required starting salary (B28) such that the net present value of the investment (B34) is equal to zero. When the NPV of an investment is equal to zero, it is correctly priced. Thus, we’re finally getting to the meat of the analysis.

Click on cell B34. Click the “Data” tab in Excel 2007. Click “Solver” on the far right. If it’s not there, it may need to be installed as an add-in. (Google it.) The target cell should already be set to $B$34. Click the “Value of:” ratio button and set it equal to zero. Set “By Changing Cells:” equal to $B$28. Click “Solve” and click “Okay.”

The value in cell B28 is the salary you will need to earn to make law school an economically sound investment. You should run solver again using at least two higher discount rates. Average the resultant salaries.


Brief Interpretation

If you’ve made it this far, I’ll conclude the analysis. I would go into detail about the economic interpretation of the second approach, but we’re already a bit long. Thus, I’ll just get to the point.

Both approaches spit out a required starting salary. If you can rationally expect to earn this salary, law school is a good bet. If you can’t, it’s a bad bet. But what salary can you expect? Again, this is probably the hardest part. An obvious starting point is just to make a subjective guess. A better approach might be to look at the recent NLJ250 stats plus outdated and highly controversial clerkship figures (http://top-law-schools.com/forums/viewt ... 1&t=108528). Let’s say you’re looking at the University of Michigan. An expected salary could be calculated as:

Expected salary = Prob(Biglaw/Clerkship)*145,000 + (1 – Prob(Biglaw/Clerkship))*50,000 = .649 * 145,000 + (1 - .649)*50,000 = $111,655

hth

[jawsthegreat]

Holy wall of text.

[Reinhardt]

Your index number accounts for about 1/4 of an explanation of the average student's grades in LS. Students who choose to attend schools at sticker are more likely to have lower index numbers, and thus do worse on average, which may lead them to have worse job choices, in which case the placement statistics for the school are overly optimistic if used as a straight "chance of getting clerkship" or "chance of getting biglaw."

[Bronte]

Your index number accounts for about 1/4 of an explanation of the average student's grades in LS. Students who choose to attend schools at sticker are more likely to have lower index numbers, and thus do worse on average, which may lead them to have worse job choices, in which case the placement statistics for the school are overly optimistic if used as a straight "chance of getting clerkship" or "chance of getting biglaw."

I think you may be misinterpreting the purpose of my post. I am not presenting results. I am presenting a method. All the numbers in the screenshots are essentially dummy variables. This method can be customized for any school, at any scholarship level / price, and all the assumptions are adjustable.

Edit: for clarity.

[coherentowst]

There are no jobs.

[Bronte]

There are no jobs.

You should be outright banned for quoting that whole post.

[catharsis]

Bronte, I'll be the first to admit that I'm horrible with numbers, percentages, and stats no matter how simple they may be. With that said I skimmed your post because I'm extremely tired but I'm also very grateful that you shared it with us because I'm sure I'll come back to (try) and use it.

Thanks!

[Bronte]

Bronte, I'll be the first to admit that I'm horrible with numbers, percentages, and stats no matter how simple they may be. With that said I skimmed your post because I'm extremely tired but I'm also very grateful that you shared it with us because I'm sure I'll come back to (try) and use it.

Thanks!

I'll be happy to field any questions via PM or in this thread. (I can just email anybody the spreadsheet.)

[Reinhardt]

Oh, I guess my point was a caution for people who would use the second spreadsheet to not be overly optimistic if they're thinking of attending for sticker.

[ViIIager]

Thanks to the OP for this--I'm always a huge supporter of thinking through the LS decision by looking at the financial costs and benefits. +1 to you buddy!

[insidethetwenty]

Looks like somebody got an "A" in Intermediate Accounting!

[narkizopoint]

Yaaarrrgghhhh! Numbers! My eyes, my eyes! Curse you, you horrid beast!

[awesomepossum]

who the hell pays 180k in 2.5 years?

[ozarkhack]

Maybe I missed it, but don't forget FICA. It adds up.

[Sky'stheLimit]

A) 28% is a retarded income tax rate. Here are the income tax rates for 2010, and if you're married, you can file jointly, so double everything.
10% Not over $8,375
15% $8,375 – $34,000
25% $34,000 – $82,400

so:
10% * 8,750= 875
15% * 25,250 (34,000-8,750)= 3,787.50
25% * 6,000 (34,000-40,000)= 1,500

Total federal income tax liability = 6,162.5 or 6162.5/40,000= 15.4%

B) Who expects to repay their student loans over 2.5 years? Law school is a LONG-TERM investment.

[Sky'stheLimit]

Thanks to the OP for this--I'm always a huge supporter of thinking through the LS decision by looking at the financial costs and benefits. +1 to you buddy!

His "financial cost and benefits" approach is ridiculous.

Also, law school has an intrinsic value (like your dream is to become an attorney, etc) that you can't assign numbers too, so a simple cost/benefit analysis wont work for people who really want to be attorneys.

[jaudette]

A) 28% is a retarded income tax rate. Here are the income tax rates for 2010, and if you're married, you can file jointly, so double everything.
10% Not over $8,375
15% $8,375 – $34,000
25% $34,000 – $82,400

so:
10% * 8,750= 875
15% * 25,250 (34,000-8,750)= 3,787.50
25% * 6,000 (34,000-40,000)= 1,500

Total federal income tax liability = 6,162.5 or 6162.5/40,000= 15.4%

B) Who expects to repay their student loans over 2.5 years? Law school is a LONG-TERM investment.

First, your forgetting FICA with is automatic 7.25% on top of everything else. Plus applicable state.

Second, I had heard accrued interest on edu loans is deductible on fed income taxes. Can anyone confirm, and is this a common state practice too?

[sanpiero]

First, your forgetting FICA with is automatic 7.65% on top of everything else. Plus applicable state.

Second, I had heard accrued interest on edu loans is deductible on fed income taxes. Can anyone confirm, and is this a common state practice too?

Fixt

[sanpiero]

B) Who expects to repay their student loans over 2.5 years? Law school is a LONG-TERM investment.

OP is assuming a 35 year career. You are misunderstanding the nature of a PV calculation

[jaudette]

I took the initiative, it looks like you can write off up $2,500 in Fed Inc Tax for paying interest on student loans. There's some limitation on qualifying income, but it looks like its easy to meet if you're married.

[Bronte]

who the hell pays 180k in 2.5 years?

Remember guys--please--these are not results. Thus, looking at my spreadsheet and saying, "this number is wrong" is not constructive. I am not saying that the assumptions are right. It's meant for you to add your own assumptions.

However, in regards to the 2.5 years, that 2.5 years was the result of a minimization calculation. I set salary equal to $160,000 and then minimized the term of the loan using Solver. This means 2.5 years is the fastest you could pay down the loan if you wanted $40,000 to live on and were making $160,000. This was just an experiment; it's good to fool around with the numbers.

But, to answer your question anyway (at my own peril), paying down the loan as fast as possible is a good thing, not a bad thing. You guys are making it sound like paying down your loan quickly is somehow a betrayal to the investment. Do you realize that paying down a $200,000 loan over a 10 year terms at 8% interest results in roughly $100,000 of interest payments?

His "financial cost and benefits" approach is ridiculous.

Also, law school has an intrinsic value (like your dream is to become an attorney, etc) that you can't assign numbers too, so a simple cost/benefit analysis wont work for people who really want to be attorneys.

I'm not sure which approach you mean, but I'll assume you mean the second one. It's an interesting point you make, and a good one. Law school isn't all about making money! Some people actually want to be lawyers to help people and to fulfill themselves. Agreed.

This does not invalidate economic analysis. You should still look at the numbers. In fact, one of the reasons that I've used slightly lower discount rates than Mr. Schlunk (please note also, then, that this is not "my 'financial costs and benefits approach'" but, rather, Vanderbilt Law Prof. Schlunk's) is to account for that "intrinsic value premium" or the "I-want-to-be-a-lawyer" factor.

[ruleser]

A) 28% is a retarded income tax rate. Here are the income tax rates for 2010, and if you're married, you can file jointly, so double everything.
10% Not over $8,375
15% $8,375 – $34,000
25% $34,000 – $82,400

so:
10% * 8,750= 875
15% * 25,250 (34,000-8,750)= 3,787.50
25% * 6,000 (34,000-40,000)= 1,500

Total federal income tax liability = 6,162.5 or 6162.5/40,000= 15.4%

B) Who expects to repay their student loans over 2.5 years? Law school is a LONG-TERM investment.

From experience (I am currently working and earning six figures) I'd say 28 percent is too low, not too high for our purposes. If the goal is to know how much you will have left take-home, the number I've found to be accurate for years is about 64% of pay. Federal tax alone doesn't mean much. There is soc secu, medicare, state tax, stae disabil, state health tax, health care premium, other benefits deductions, sometimes local/city tax. No matter how you slice it, generally multiplying what you earn by .64 seems to get it about right, so sort of an effective 36 % tax/payroll deduction rate.

As for B, Hey, if you could keep living like a student cost-wise and knock out your loans in 3 years, why not - but ite I'd change those numbers to put in the bank a couple g's a month as rainy day/layoff insurance - something almost no one works into their budgets. Saving is no longer a luxury, its required to get up to 1 year $ in the bank asap if you don't want to risk homelessness these days.

Edited for typos

[Bronte]

From experience (I am currently working and earning six figures) I'd say 28 percent is too low, not too high for our purposes. If the goal is to know how much you will have left take-home, the number of founf to be accurate for years is about 64% of pay. Federal tax alone doesn't mean much. There is soc secu, medicare, state tax, stae disabil, state health tax, health care premium, other benefits deductions, sometimes local/city tax. No matter how you slice it, generally multiplying what you earn by .64 seems to get it about right, so sort of and effective 36 % tax/payroll deduction rate.

As for B, Hey, if you could keep living like a student cost-wise and knock out your loans in 3 years, why not - but ite I'd change those numbers to put in the bank a couple g's a month as rainy day/layoff insurance - something almost no one works into their budgets. Saving is no longer a luxury, its required to get up to 1 year $ in the bank asap if you don't want to risk homelessness these days.

Ruleser, thanks. People should take note of this and potentially use your effective tax rate estimates.

However, your comment made me notice a bigger error in the spreadsheet. I wasn't taxing the after law school salary in Approach 2, which is a big snaffu. I've updated the article to fix this error. It's a work in process so I'm happy to take constructive criticism. In general, I think it's good for people to at least fool around with the first approach, which is very simple and very relevant.

[realworldescapee]

I would only add that if one wanted a more accurate picture, there would be a built-in tuition increase of at least 5% (some schools have more) but it's a faulty assumption that tuition remains stagnant throughout your LS years.

Hopefully this gets people to take scholarships more seriously. For me to break even with my scholarship offers at multiple schools according to this analysis I have to make roughly 35,000 a year and these are schools I'd have no problem going to.

One thing I'd like to see added (I don't know enough of the math to do it myself) is to see how all of this works if you are in an LRAP. One of the reasons I'm considering taking schollys at 'lower-ranked' (compared to where I've gotten into) schools is the flexibility to enter the public sector. If some part or all of your loans can be forgiven then that changes the equation as well.

Thanks for the tool.

[Bronte]

I would only add that if one wanted a more accurate picture, there would be a built-in tuition increase of at least 5% (some schools have more) but it's a faulty assumption that tuition remains stagnant throughout your LS years.

Hopefully this gets people to take scholarships more seriously. For me to break even with my scholarship offers at multiple schools according to this analysis I have to make roughly 35,000 a year and these are schools I'd have no problem going to.

One thing I'd like to see added (I don't know enough of the math to do it myself) is to see how all of this works if you are in an LRAP. One of the reasons I'm considering taking schollys at 'lower-ranked' (compared to where I've gotten into) schools is the flexibility to enter the public sector. If some part or all of your loans can be forgiven then that changes the equation as well.

Thanks for the tool.

LRAPs are more about the specific program than the math. I honestly don't know how they work, but if someone explained how they work we could probably find a way to factor it into the analysis. Adding the tuition increase would be no problem.