Top Law Schools

I broke this down in detail, please excuse it's length. These are small bits of game 2.

Rule 1. EIther N or P must be selected, but N and P cannot both be selected.

Which is correct?

A. The necessary condition is negated.

N -> ~P

P -> ~N


B. The sufficient condition is negated.

~N -> P

~P -> N

C. Both are fine. If so, please explain why to me!

The next rule...

Rule 2: N cannot be selected unless L is selected.

Rule:
N -> L

Contrapositive:
~L -> ~N

To combine rules 1 and 2, I have been taking the contrapositive of rule 2 and the negated sufficient condition version of rule 1 to get:

~L -> ~N -> P

contrapositive:

~P -> N -> L

Is this correct?

From what PT is?

gdane5 wrote:From what PT is?

9.

In any case what I got from this is, "If L is selected, then N is selected and P is not selected". "If L is not selected, than N is not selected and P is selected".

gdane5 wrote:In any case what I got from this is, "If L is selected, then N is selected and P is not selected". "If L is not selected, than N is not selected and P is selected".

Here's my hang-up: rule 1, the either/or statement: I thought the negated term HAD to be the necessary condition. Yet to make this work, it was the sufficient condition.

Compare it to this:

3. Either J or K must be selected, but J and K cannot both be selected.
J->~K

OR

K->~J

4. Q cannot be selected unless K is selected.
RULE:
Q->K

CONTRA:
~K->~Q

To combine:

Q->K->~J

J->~K->~Q

These rules are from the same game. Both use either/or statements while negates the necessary condition and the other negates the necessary condition. What is getting me is that I thought it has to be one or the other. In other words, to make these chains I have to change my negation on the first rule to fit the need: is that legitimate since these are either/or statements?

Ok im going to take a look at this game. Ill try to come back on here soon.

Ok so i took a look at it. I answered the questions, but honestly I didnt diagram a lot of the contrapositives and all that. Were there any questions that you didnt understand or were you just having problems diagramming and with the rules?

It was the either/or rules. One required that negate the sufficient condition, while the other required that I negate the necessary condition to make the chains work. I thought that it had to be on way or the other, period.

When diagramming an either/or rule like the two above, do you always negate the sufficient side, necessary side or does it not matter?

Oh man I really dont know. I dont want to confuse you or give you bad advice so I'll let someone else answer this.

youknowryan wrote:I broke this down in detail, please excuse it's length. These are small bits of game 2.

Rule 1. EIther N or P must be selected, but N and P cannot both be selected.

Which is correct?

A. The necessary condition is negated.

N -> ~P

P -> ~N


B. The sufficient condition is negated.

~N -> P

~P -> N

C. Both are fine. If so, please explain why to me!

The next rule...

Rule 2: N cannot be selected unless L is selected.

Rule:
N -> L

Contrapositive:
~L -> ~N

To combine rules 1 and 2, I have been taking the contrapositive of rule 2 and the negated sufficient condition version of rule 1 to get:

~L -> ~N -> P

contrapositive:

~P -> N -> L

Is this correct?

You ended up at the right place (both diagrams together represent the rule), but there's an easier way to think about it. Break it into two parts, since it is essentially two rules in one.

Either X or Y must be selected.
Therefore, if X is not selected, Y must be selected.
~X → Y; ~Y → X (contrapositive)

X and Y cannot both be selected.
Therefore, if X is selected, Y cannot be selected.
X → ~Y; Y → ~X (contrapositive)

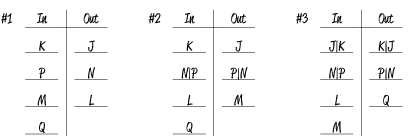
One approach to the game is to set up scenarios. Exactly two of PN and exactly two of JK must be in, and exactly two of each pair must also be out. You can set up a scenario for each one of L, M, and Q occupying the third out slot. You should end up with seven possible solutions.
(LinkRemoved)